
Ecology Letters | 写给实践生态学家的β多样性分析指南
导读
生态学里,对于多样性的关注,似乎永远不会过时。而在群落生态学分析里,β多样性的地位毋庸置疑。随着研究的深入,β多样性的概念内涵越来越广泛,度量指标越来越多,计算方法也越来越多,也引起了一些争议和问题。例如,是否需要这么多指标,能统一成一个指标吗?不同的指标、不同的计算方法有什么差异?该如何选择?选择的依据是什么?
这篇大咖云集、略微古老(2011年)、高引用率(1581 citations)的文献详细叙述了,截至2010年的相关研究认知;时至今日,对于理解、计算和应用β多样性依然有很好的帮助作用。本文详细介绍了β多样性的概念、内涵、度量指标、计算方法、选择依据,等等。
▉ 原文信息

▉ 原文摘要
A recent increase in studies of β diversity has yielded a confusing array of concepts, measures and methods. Here, we provide a roadmap of the most widely used and ecologically relevant approaches for analysis through a series of mission statements. We distinguish two types of β diversity: directional turnover along a gradient vs. non‐directional variation. Different measures emphasize different properties of ecological data. Such properties include the degree of emphasis on presence/absence vs. relative abundance information and the inclusion vs. exclusion of joint absences. Judicious use of multiple measures in concert can uncover the underlying nature of patterns in β diversity for a given dataset. A case study of Indonesian coral assemblages shows the utility of a multi‐faceted approach. We advocate careful consideration of relevant questions, matched by appropriate analyses. The rigorous application of null models will also help to reveal potential processes driving observed patterns in β diversity.
▉ 正文
Part 1: turnover and variation
本文把β多样性分成两类进行讨论,turnover和variation(图1)。Turnover,强调群落结构沿着某个梯度而变化,可以是环境梯度、空间梯度、或者时间梯度,为有方向性的变化。Variation则是指在特定区域(或者特定梯度范围)内,群落结构的变异,方向性较弱或者没有方向性(有点类似于,统计学里,若干个相近值或者临近值的离散性)。
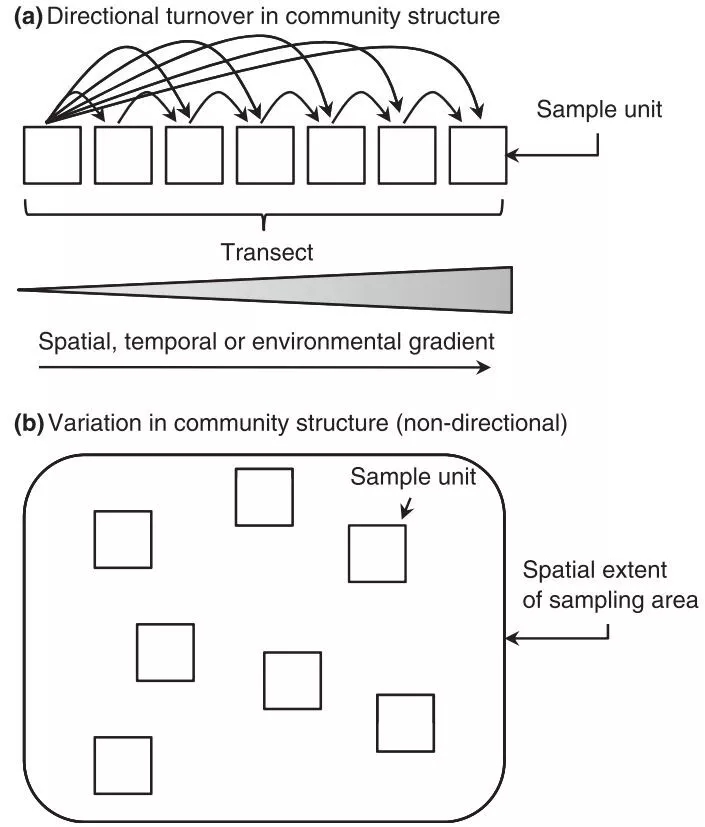
Part 2: measures of β diversity
度量β多样性的指标,主要有两类,传统方法和基于群落的方法。传统方法主要是指,β=γ/α,这是Whittaker最早提出的计算方式。在此基础上,还有一些改进版,例如考虑物种丰度的方法,βShannon= Hγ⁄Hα。
基于群落矩阵的计算方法,是现在使用比较多的。假设群落为矩阵Y,共有N行(n个样点),p列(p个物种)。使用Δy表征两个群落之间的差异,这是最简单的β多样性。考虑到梯度(用x表示)时,则β多样性可以理解为群落结构沿着梯度的变化速率。
Part 3: statements and analyses
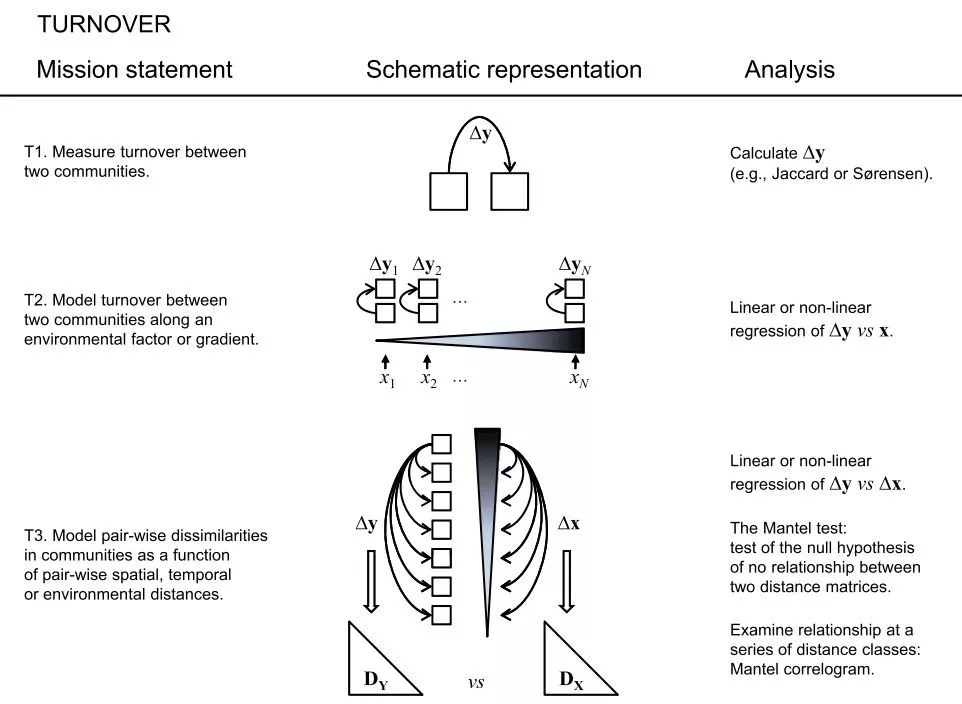
鉴于β多样性分析涉及的情形各异、复杂性多样,本文用简洁的图示,展示了不同的情形,以及对应情形下计算方法的选择。从T1到T6,V1到V6,对应的复杂性依次升级。
首先来看一下turnover(图2)。T1是最低级版本的β多样性,即,两个群落的差异。T2是T1的升级版,当有一个梯度存在时,每个梯度的截面上,各有两个群落,此时的β多样性可以升级为“两两差异”对梯度的响应关系。T3是T2的改良版,假设对应每个梯度截面仅有一个群落,此时β多样性可以升级为“群落的两两差异”与“梯度的两两差异”的相关性。比如我们经常会使用Mantel检验,检测群落的变异与梯度的变异是否具有相关性,再考虑后续处理。
T4-T6是较为复杂的情形(图3)。假设群落变异与梯度变异有较好的相关性,则在T3的基础上进一步分析,解析“群落变异”对“梯度变异”的速率,即经常谈论的“距离衰减关系”(DDR)。DDR是指,随着距离的增大,相距越远的群落,相似性越低(这里的距离,可以是空间距离,也可以是环境或者空间)。
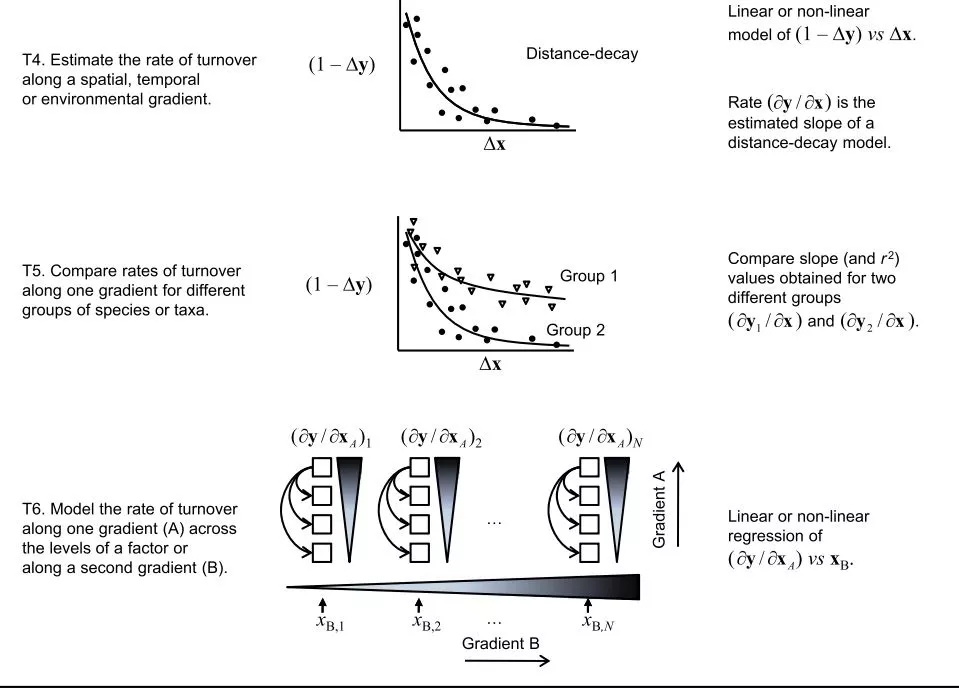
截至到T4,实际上已经完成了常规的β多样性分析过程。T5相当于是一个应用场景。例如,我们有时候可能会关心不同类型的生物对同一梯度的响应灵敏度。不同生物的响应速率经常可能不一致。在管理和应用层面的意义就是,单一的指示生物未必足够,往往需要综合的指示生物。截至目前,讨论的都是一个梯度。复杂程度继续升级的话,就是在T3的基础上,涉及多个梯度。
Variation情形下的分析方式略有不同(图4)。因为variation的方向性不明确,一般会按照V2的方法(PCA或NMDS等),对群落进行排序。排序结果可能会把一堆群落分成若干个簇(cluster)。这种分簇现象,实际上也可以理解为,反映了梯度的存在。所以,才会有V3的分析,根据RDA等方法,解析环境因子(或者其他因子)对群落变异的影响;并进而根据变差分解(variation partitioning)等方法,解析不同因素对群落变异的贡献程度。
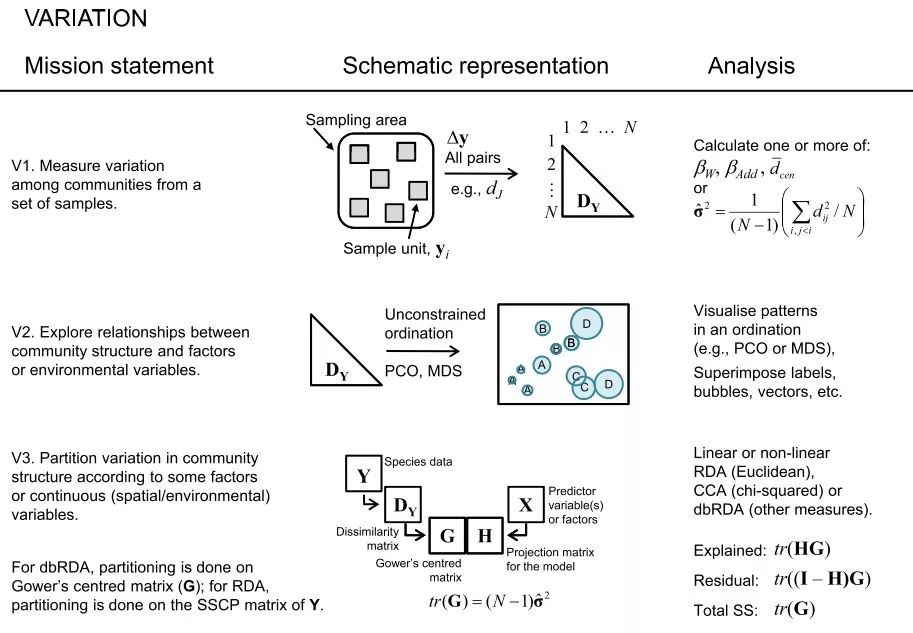
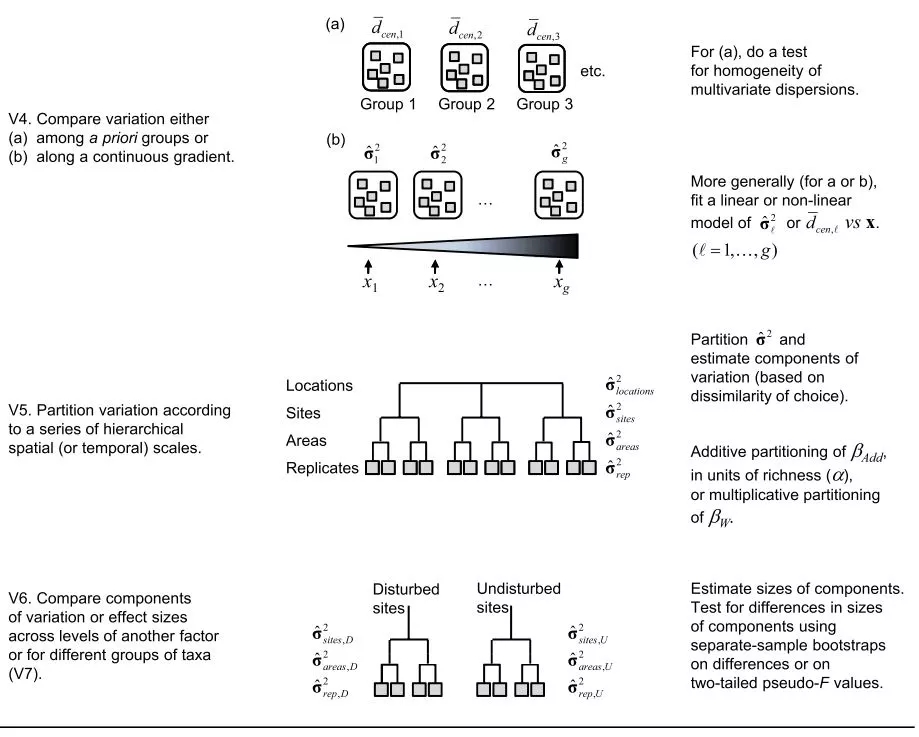
(综合来说,turnover的分析步骤,比较适合梯度比较清晰的情况。然而,生态学取样时,有时候梯度并不是那么明显。因此,经常会先使用variation所涉及的方法,对群落(以及因子)的变化趋势做个综合分析,如果有梯度的,再转化到梯度分析上,或者综合使用两类分析方法)。
Part 4: key properties
另外,本文还提到了几个需要注意的事项。
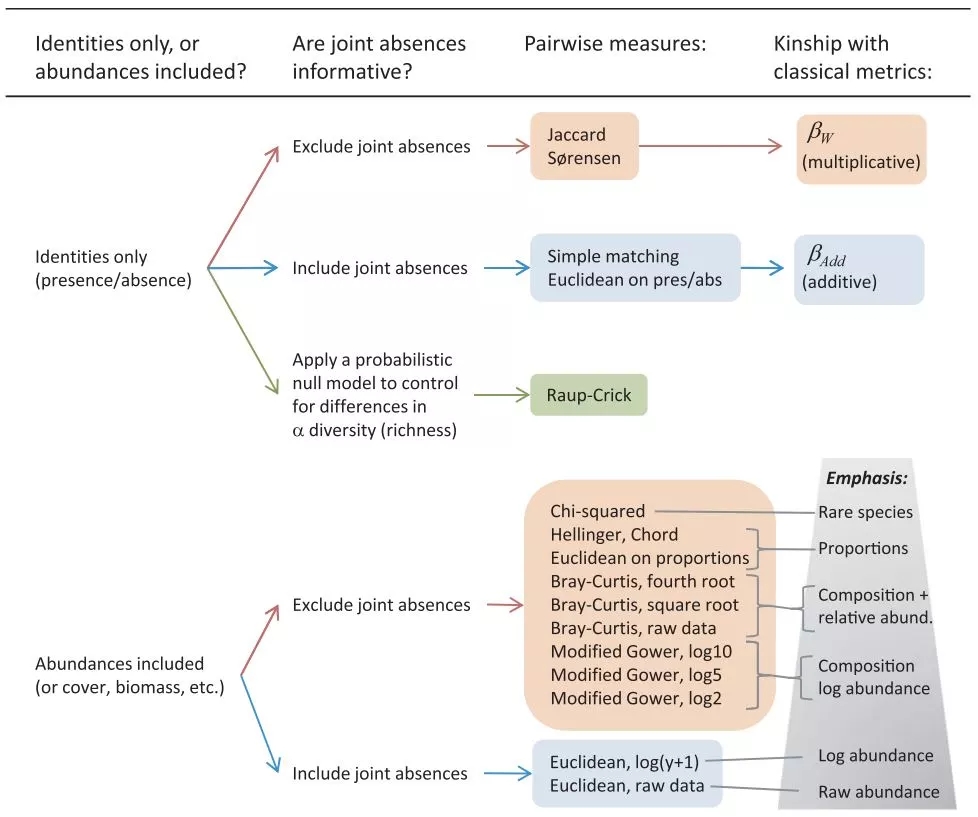
第一,数据类型的问题。使用有无(presence / absence)数据(不考虑丰度)和丰度(relative abundance)数据(同时考虑物种的有无和丰度),可能会得到不太一样的结果,需要注意。
第二,相邻缺失问题。两两群落比较时,两群落共有组分为a,群落1特有的组分为b,群落2特有的组分为c,两群落都没有的组分为e。我们常用的计算方法是不考虑e的,并且忽略e对结果可能影响不大。但是,一些特殊情况下,可能需要考虑e。比如从γ多样性的角度考虑时,尤其是群落间共有群落越来越少时,纳入或者不纳入e的计算方法,结果差异还是蛮大的。
第三,常规的计算方法里,β多样性总是会受到α多样性的影响。而零模型可以解决这个问题。零模型的原理是,固定α多样性的情况下,从原始物种库里随机抽样,比较随机抽取的结果与实际群落的差异,得到的概率值。
基于上述分析和注意事项,本文提供了一张概念图,可以作为选择计算方法的参考(图6)。
最后提供了一个案例,可以直观看出,不同的计算指标,得到的结果差异确实挺大的(图7;图8)。案例涉及的是珊瑚群落。1981年为干扰前。1982年发生了严重的白化事件。1982和1983年为干扰后的群落。详情参见原文。
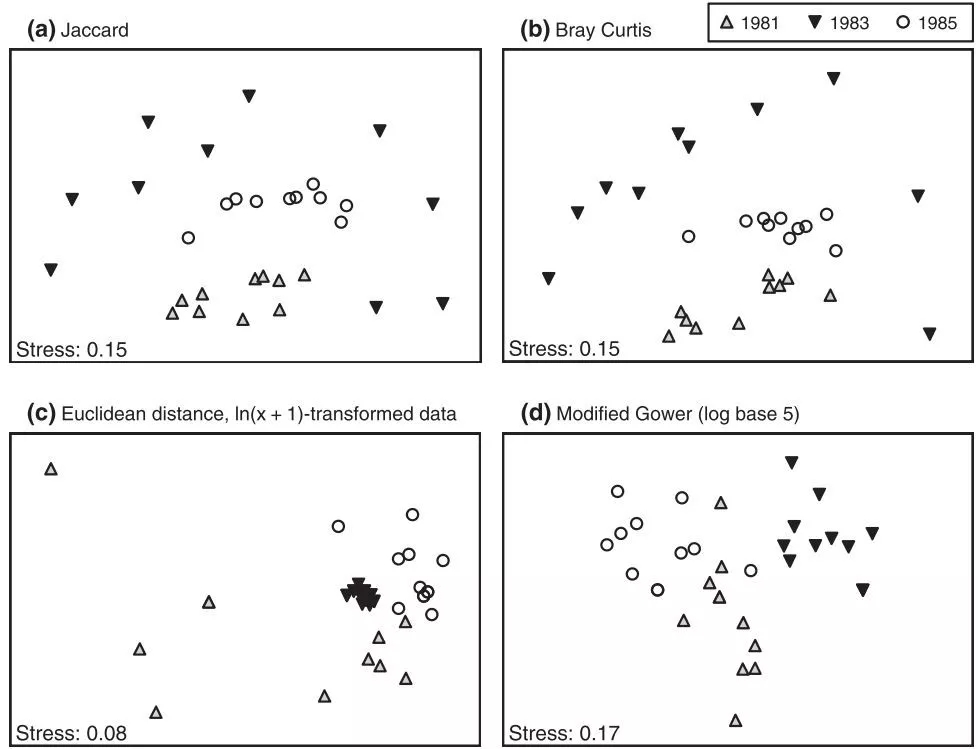
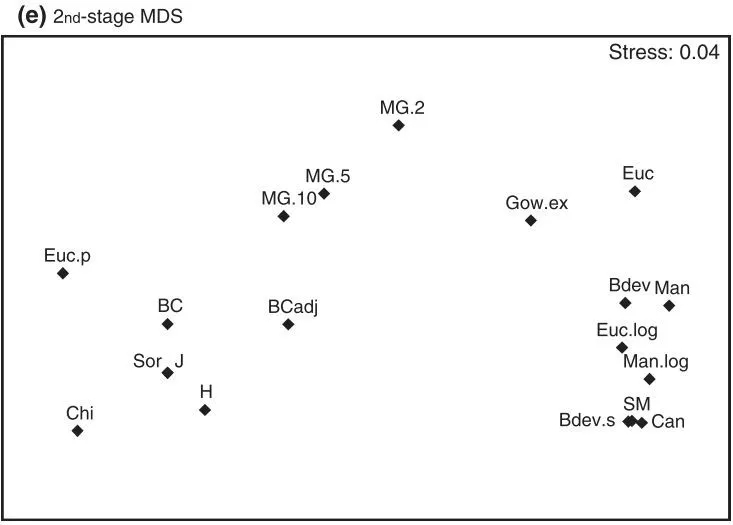
图8. 不同计算方法的差异(二)
▉ 编辑寄语
第一,许是出于叙述表达的简洁要求,本文只用了广义的turnover一词,表示群落结构的变化,而没有刻意区分turnover(周转)和nestedness(嵌套)。实际上,在本文里,turnover包含了nestedness的内涵。狭义的理解上,turnover和nestedness是贡献β多样性的两个组分,可以用如下所示的概念图来理解(图9;Baselga 2010a; 2010b)。Turnover过程,强调了物种的替换(species replacement);而nestedness强调了物种的获得(species gain)或者丢失(species loss)。实际上,Baselga还构建了计算这两个组分的方法,并提供了相应的R语言包,betapart。解析二者的相对重要性还是有意义的,可以更详细地理解和认识观测β多样性(observed β diversity)究竟是什么过程引起的。

图9. Turnover和nestedness概念图(Baselga 2010a)
第二,本文重点强调了基于群落组成与结构的β多样性。实际上,与广义的α多样性类似,越来越多的研究在推广广义的β多样性,例如功能多样性、遗传多样性等等。例如纳入遗传多样性的方法,会考虑物种的进化地位(遗传发育关系)所形成的β多样性。有条件的话,适当多考虑一些多样性组分(different components of β diversity),对于现象的理解和认识还是有帮助的。
第三,β多样性的度量指标是比较多的。本文的作者们认为,多重性是有必要的,而没有必要统一只用一个指标。个人比较赞同这个观点。如果不同指标计算的结果一致性非常好,可能说明现象或者变化比较明显(或者说是数据比较好?)。而如果一致性不那么好的话,也没有关系,说明不同层面的响应确实可能有异质性。多重性实际上给我们提供了多角度看待问题的思路和方法。
第四,本文重点强调了零模型(null models)的重要性。零模型现在已经用的比较普遍了,尤其是用于区分随机性过程和决定过程(本公众号之前已有相关介绍)。本文作者之一James Stegen等人基于零模型、Raup-Crick距离、遗传距离等,构建了一套方法解析影响群落的生态学过程(ecological processes)(图10;Stegen et al. 2013; 2015),并得到进一步的推广演化。目前主要包括五个过程:变量选择(也称为异质化选择,heterogeneous selection),同质化选择(homogeneous selection),扩散限制(dispersal limitation),同质化扩散(homogenizing dispersal),以及非主导性过程(Undominated)。目前也已经有不少文章在实践和使用(图11;Yan (颜庆云老师)et al. 2016)。
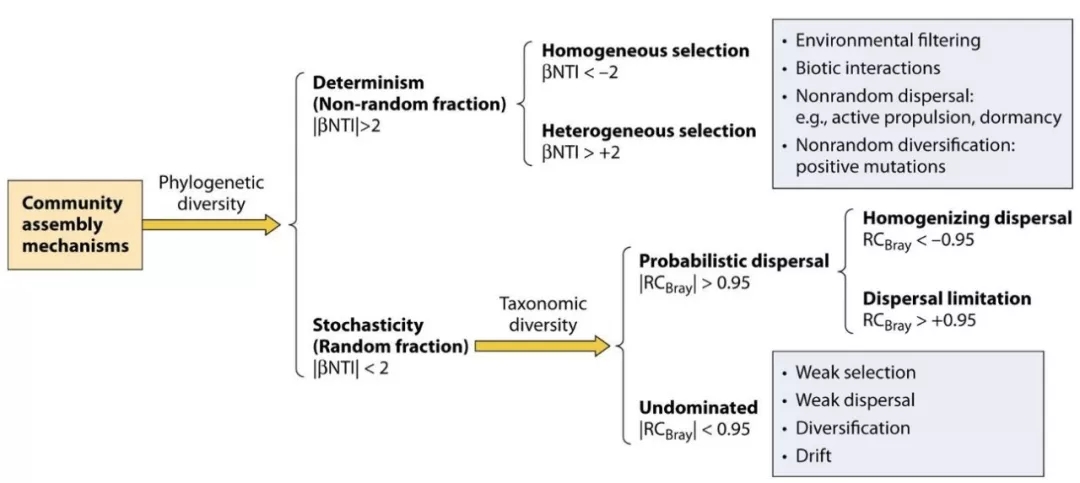
图10. 生态学过程区分的概念图(Zhou & Ning, 2017)
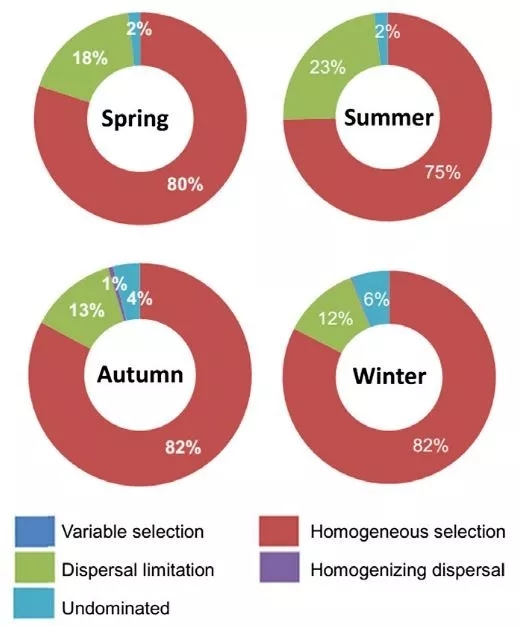
图11. 生态学过程贡献比例的拆分(Yan et al. 2017)











